费马大定理的证明者-狄利克雷

今天我们讲一位非常著名的数学家，他就是约翰·彼得·古斯塔夫·勒热纳·狄利克雷，狄利克雷是德国数学家，他对数论，数学分析和数学物理都有着非常突出的贡献。狄利克雷同时也是解析数学的创始人之一。

在1805年狄利克雷出生于迪伦，在狄利克雷中学的时候就得到了物理学家欧姆的影响并且在1822年至1826年在巴黎求学受到了傅里叶的影响。在回到自己的国家之后狄利克雷在布雷斯劳大学，柏林军事学院和柏林大学任教27年。

在分析数学方面狄利克雷是最早提倡严格化方法的数学家之一，狄利克雷在1837年首次提出函数是X乙y之间的一种对应关系的现代观点。在数论方面狄利克雷是高斯思想的传播者和推广者，在1863年狄利克雷撰写了自己的著作并且对高斯的著作也进行了非常清晰并有独特见解的解释。这使得高斯的思想得到了广泛的传播，在1837年狄利克雷构建了狄利客雷级数，并且在1838年至1839年狄利克雷首次确定的二次项系数的公式。

狄利克雷在数论方面有着一定的贡献，狄利克雷对高斯的著作进行了研究，并且提出了新的解释。对费马大定理狄利克雷给出了当n＝14无整数解证明并且还探讨了二次项，多项式的因子，二次和双二次互反德等等的问题并且狄利克雷还开创了解析数论研究。

在1842年狄利克雷开始研究具有高斯系数的型，并且首次运用了盒子原理。而这个原理也在现代数论中起到了决定性的作用。在1846年狄利克雷在属于代数数论的单元理论的文章中获得了一个漂亮且完整的结果这个也被称为狄利克雷单元定理。

在分析方面狄利克雷最突出的贡献是对傅立叶级数收敛性的研究，在1822年至1825年期间狄利克雷在巴黎会议上见到傅立叶之后，并且就对傅里叶级数产生了兴趣。狄利克雷之后也给出了关于傅里叶级数的收敛性证明。

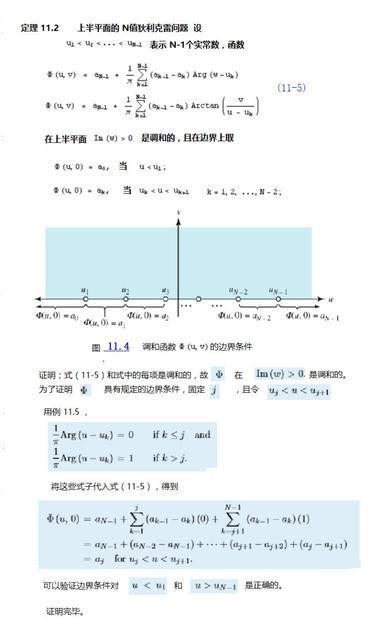
在1837年狄里克雷又再次回到了三角级数理论的研究上，并且发表了一系列的文章其中拓展了当时普遍采用的函数概念。并且引入了现代函数的概念。但狄利克雷来的连续函数概念仍然是直观的，并且根据等距取函数值求和的方法定义积分。并且在此基础上狄利克雷建立了傅里叶级数的理论。

狄利克雷在数学和力学上都做出了重大的贡献，尤其是在分析，数论，位势论。最为突出在1839年狄利克雷发表了三部涉及力学的数学论文。并且讨论了多重积分估值的方法用于确定椭球体对其内部和外部任意质点的引力。并且狄利克雷开始对数学物理问题的研究。狄利克雷在1850年首先提出了和研究了拉普拉斯方程的边值问题。

狄利克雷有着许多的贡献，比如狄利克雷定理，狄利克雷单位定理，狄利克雷卷积，狄利克雷特征，狄利克雷函数，狄利克雷分布，狄利克雷级数，狄利克雷积分，狄利克雷判别法，狄利克雷核，狄利克雷边界条件等等。

在1855年高斯去世的时候，狄利克雷在高斯的纪念演讲会上突发心脏病。虽然狄利克雷在返回途中已经恢复了一些。但在病中的狄利克雷听到了自己夫人中风身亡的打击，病情更加加重于是在1859年狄利克雷逝世。

谢谢各位看官的欣赏你对狄利克雷有什么认识和了解，请留下你的评论！如果喜欢请关注，转发，收藏！谢谢！我们下期再见。